누가 활성화 함수와 손실함수가 뭐냐고 물어보면
뭐라고 해야될까
일단은 활성화함수부터 말해야겠지
우선 저번 블로그때 말했던 내용을 다시 보여줄게
""""
영어로는 activation function이라고 해
과학시간에 뉴런 배웠던 거 생각나?
자극, 활성화 이런 단어들이 있었잖아
사실 나도 기억이 잘 안나는데
그런 느낌이야
뉴런을 모방해서 만든 인공신경망이잖아
입력으로 받은 신호의 합이 임계값을 넘을 경우에만
뉴런이 활성화 되어서 출력 신호를 발생해
아까 w는 weight 가중치
b는 bias 편향이라고 얘기했는데
이제 더 자세하게 말할 때가 온 것 같아
w 가중치
입력이 출력에 얼마 만큼 영향을 주는 지 결정해
가중치가 크면 입력 신호의 영향이 커지는 거야
예를 들면 y=4x+4 랑 y=24x+4가 있으면
x는 입력신호, 첫번째 식의 가중치는 4,
두번째 식의 가중치는 24
x=2일때 처음꺼는 4*2+4고, 두번째꺼는 24*2+4 잖아
이렇게 가중치가 큰 두번째꺼가
입력신호의 영향을 많이 받게돼
bias 바이어스
아까 계산할때는 바이어스까지는 고려하지 않았는데
편향이라는 게 어느 한 쪽으로 치우치게 하는 거잖아
바이어스는 출력을 어느 한 쪽으로 치우치게 해서
얼마나 쉽게 활성화가 되는 지를 결정해
아까 활성화 함수 처음 설명하면서
뉴런이 임계값을 넘으면 활성화 된다고 했잖아
b가 임계값이야
x1w1 + x2w2 + x3w3 + b1 >0 이면 활성화가 된다고 하자
만약에 b가 -0.01이면 x1w1 + x2w2 + x3w3이
0.01만 넘으면 활성화가 돼
근데 b가 -100이면 x1w1 + x2w2 + x3w3 -100
왼쪽에 있는 식의 입력 신호가 다 0이 되더라도
b때문에 출력이 0이 아니게 되는거야
이런 의미로 바이어스는 출력을 어느 한 쪽으로 치우치게 해
"""
조금 더 추가설명을 하자면,
모든 입력 신호를 무조건 전달하지 않고
특정 입력 조건에서만 활성화 해
만약에 손이 뜨거운 물건에 닿으면
감각 뉴런이 활성화되어 뇌에 통증 신호를 전달해
모든 입력 신호를 다 활성화되면 안되는 이유를 알겠지
중요할때만 해야돼
이런 것 처럼,
인공신경망에서는 활성화 함수를 사용하면
입력 데이터에서 중요한 특징만을 학습할 수 있어
더 자세하게 말하려면
초기 인공신경망인 퍼셉트론에 대해
먼저 설명을 해야될 것 같아
활성화 함수가 퍼셉트론에서 처음 등장했거든
초기 인공신경망인 퍼셉트론,
이때 활성화 함수가 왜 필요했을 까?
이걸 알기 위해서는
퍼셉트론의 학습 과정을 알아야 돼

(퍼셉트론에는 역전파가 없어)
입력과 가중치를 곱한 값들에 바이어스를 더해서
활성화 함수에 넣어

퍼셉트론에서는 활성화 함수로
계단함수를 사용해
총 합이 0보다 크면 1 (활성화)
그렇지 않으면 0 (비활성화)을 출력해
그리고 출력값이 정답과 다르면
wi←wi+η⋅(y_true−y_pred)⋅xi
이렇게 가중치를 업데이트 해
y_true는 정답값
y_pred는 출력값이야 (예측값)
η 이건 학습률이야
얼마나 빠르게 학습을 진행할 지 결정해
자 퍼셉트론으로
AND 데이터를 학습해보자
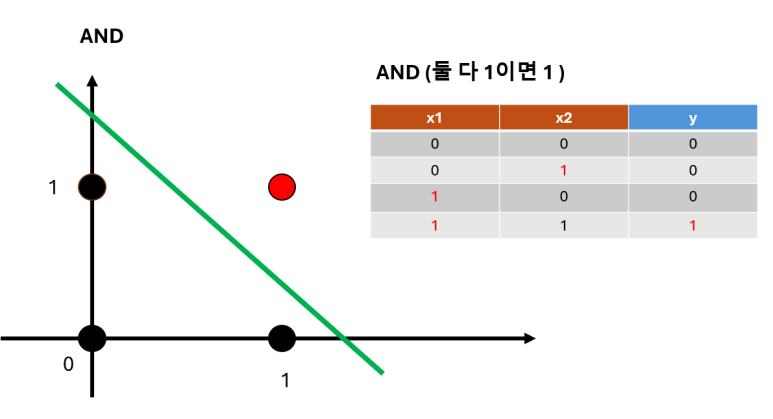
(뭐랄까 시리즈 1탄에서 썼던 그림이야)
(chat gpt에게 부탁한 코드)
코드를 일단 한번 봐바
import numpy as np
# 퍼셉트론 클래스 구현
class Perceptron:
def __init__(self, input_size, learning_rate=0.2, epochs=10):
self.weights = np.zeros(input_size + 1) # 가중치 초기화 (bias 포함)
self.learning_rate = learning_rate # 학습률
self.epochs = epochs # 학습 반복 횟수
def activation_function(self, x): #활성화 함수 (계단함수)
return 1 if x > 0 else 0
def predict(self, inputs):
summation = np.dot(inputs, self.weights[1:]) + self.weights[0] # 선형 결합
return self.activation_function(summation)
def fit(self, X, y):
for epoch in range(self.epochs):
for inputs, target in zip(X, y):
prediction = self.predict(inputs)
self.weights[1:] += self.learning_rate * (target - prediction) * inputs # 가중치 업데이트
self.weights[0] += self.learning_rate * (target - prediction) # 편향 업데이트
# AND 게이트 데이터셋
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]]) # 입력 데이터
y = np.array([0, 0, 0, 1]) # 출력 데이터
# 퍼셉트론 모델 학습
perceptron = Perceptron(input_size=2)
perceptron.fit(X, y)
# 학습된 가중치 확인
print("학습된 가중치:", perceptron.weights)
# 예측 결과 확인
print("AND 게이트 예측 결과:")
for inputs in X:
print(f"입력: {inputs}, 출력: {perceptron.predict(inputs)}")우선
def __init__(self, input_size, learning_rate=0.2, epochs=10):
self.weights = np.zeros(input_size + 1) # 가중치 초기화 (bias 포함)
self.learning_rate = learning_rate # 학습률
self.epochs = epochs # 학습 반복 횟수__init__ 함수로 클래스를 초기화 해
input_size는 입력의 차원이야
self.weights = np.zeros(input_size + 1)
가중치를 0으로 초기화하는 거야
+1을 해주는 이유는
마지막 항으로 바이어스를 하기 위함이야
learning rate는 학습률이고
아까 말했듯이
얼마나 빠르게 학습을 진행할 지 결정해
epochs는 에포크로,
학습 반복 회수야
이거는 다음에 또 자세하게 설명할게
def activation_function(self, x): #활성화 함수 (계단함수)
return 1 if x > 0 else 0 이어서 설명하면,
activation_function 함수로
계단함수 식을 작성해
x>0 이면 1
아니면 0
def predict(self, inputs):
summation = np.dot(inputs, self.weights[1:]) + self.weights[0] # 선형 결합
return self.activation_function(summation)
predict 함수에서는,

이 과정을 수행해
입력과 가중치를 곱한 값들에 바이어스를 더해서
활성화 함수에 넣어
def fit(self, X, y):
for epoch in range(self.epochs):
for inputs, target in zip(X, y):
prediction = self.predict(inputs)
self.weights[1:] += self.learning_rate * (target - prediction) * inputs # 가중치 업데이트
self.weights[0] += self.learning_rate * (target - prediction) 그리고 fit 함수에서는
가중치 업데이트를 진행해줘
wi←wi+η⋅(y_true−y_pred)⋅xi
가중치와 편향은 따로 업데이트 하는데
b←b+η⋅(ytrue−ypred)
편향은 이렇게 업데이트 해줘
따로 업데이트를 하는 이유는
편향이 입력값과는
독립적으로 출력에 영향을 주기 때문이라고 하더라
자 이렇게 퍼셉트론 클래스를 구현했어
# AND 게이트 데이터셋
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]]) # 입력 데이터
y = np.array([0, 0, 0, 1]) # 출력 데이터
# 퍼셉트론 모델 학습
perceptron = Perceptron(input_size=2)
perceptron.fit(X, y)
X는 AND 게이트의 입력 데이터이고
y는 정답값이야
그리고
perceptron=Perceptron(input_size=2)
이 과정으로 퍼셉트론 클래스의 객체가 생성돼
초기화가 진행돼
그리고 perceptron.fit(X,y) 으로
학습을 진행해
이 함수 안에서 predict 함수가 호출되어
얻은 예측값으로 업데이트를 진행해
# 학습된 가중치 확인
print("학습된 가중치:", perceptron.weights)
# 예측 결과 확인
print("AND 게이트 예측 결과:")
for inputs in X:
print(f"입력: {inputs}, 출력: {perceptron.predict(inputs)}")
그리고 학습된 가중치를 확인하고
예측 결과 또한 확인해
가중치 w1과 w2는 각각 -0.4와 0.4가 되었고
바이어스는 0.2가 되었어
그리고 이렇게 학습된 퍼셉트론 모델에
AND 게이트 데이터를 입력하면
맞게 예측값을 출력해내는 것을 볼 수 있어
퍼셉트론에 활성화 함수가 없으면 어떻게 될 까?
아까 코드에서 활성화 함수를 지워볼게
predict 함수에서 활성화 함수에 넣지않고
그냥 바로 return을 해볼게
import numpy as np
# 퍼셉트론 클래스 구현
class Perceptron:
def __init__(self, input_size, learning_rate=0.2, epochs=10):
self.weights = np.zeros(input_size + 1) # 가중치 초기화 (bias 포함)
self.learning_rate = learning_rate # 학습률
self.epochs = epochs # 학습 반복 횟수
def predict(self, inputs):
summation = np.dot(inputs, self.weights[1:]) + self.weights[0] # 선형 결합
return summation
def fit(self, X, y):
for epoch in range(self.epochs):
for inputs, target in zip(X, y):
prediction = self.predict(inputs)
self.weights[1:] += self.learning_rate * (target - prediction) * inputs # 가중치 업데이트
self.weights[0] += self.learning_rate * (target - prediction) # 편향 업데이트
# AND 게이트 데이터셋
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]]) # 입력 데이터
y = np.array([0, 0, 0, 1]) # 출력 데이터
# 퍼셉트론 모델 학습
perceptron = Perceptron(input_size=2)
perceptron.fit(X, y)
# 학습된 가중치 확인
print("학습된 가중치:", perceptron.weights)
# 예측 결과 확인
print("AND 게이트 예측 결과:")
for inputs in X:
print(f"입력: {inputs}, 출력: {perceptron.predict(inputs)}")
그러면 이런 결과가 나오게 돼
AND 게이트는 x1=0,x2=0 일때 y=0인데
출력이 -0.16483626841185234
제대로 예측을 하지 못하게 돼
그래서 알 수 있는
퍼셉트론에서 활성화 함수의 역할은
이진분류를 해준다는 거야

계단함수는 비선형함수야
사실 처음에 헷갈려서 계단함수가 선형함수인 줄 알았어
다층 퍼셉트론 활성화함수들만 비선형함수라고 생각했지 뭐야..
비선형함수가 뭐냐면
우선 선형함수는 이렇게 생겼어

선형함수가 아니면 비선형함수겠지
비선형함수라는 게 왜 중요하냐면
활성화함수로 선형함수를 쓰지 않아
왜 그러냐면
우선 제일 대표적인 이유로는

다층퍼셉트론에서는
다층의 구조를 쌓게 되잖아,
근데 선형함수를 쓰면
여러 개의 선형함수를 써도
어차피 선형 함수 하나와 같기 때문이야
이게 무슨 소리냐면
f(x)=ax라는 선형함수가 있다고 하면
이 함수 3개를 결합한 것은 y=f(f(f(x)))잖아
근데 이걸 풀어보면 y=a*a*a*x야
그러면 그냥 f(x)=a^3x인 선형함수 하나를 쓰는 거랑 똑같잖아
그러면 다층의 구조를 쌓는 이점이 없게 돼
근데 퍼셉트론의 활성화함수인
계단함수도 비선형함수야
아까도 말했듯이
나는 사실 처음에 계단함수가 선형함수라고 생각했지 뭐야
그래서 퍼셉트론의 활성화함수도
비선형함수면 안되는 이유가 있나 궁금해졌어
찾아보니 퍼셉트론은 이진분류를 하기 위해서 설계되었다고 해
근데 활성화 함수가 선형함수이면
(코드에서 활성화함수를 y=2x+1인 선형함수로 바꿔줬어)
import numpy as np
# 퍼셉트론 클래스 구현
class Perceptron:
def __init__(self, input_size, learning_rate=0.2, epochs=10):
self.weights = np.zeros(input_size + 1) # 가중치 초기화 (bias 포함)
self.learning_rate = learning_rate # 학습률
self.epochs = epochs # 학습 반복 횟수
def activation_function(self, x): #활성화 함수 (계단함수)
return 2*x+1
def predict(self, inputs):
summation = np.dot(inputs, self.weights[1:]) + self.weights[0] # 선형 결합
return self.activation_function(summation)
def fit(self, X, y):
for epoch in range(self.epochs):
for inputs, target in zip(X, y):
prediction = self.predict(inputs)
self.weights[1:] += self.learning_rate * (target - prediction) * inputs # 가중치 업데이트
self.weights[0] += self.learning_rate * (target - prediction) # 편향 업데이트
# AND 게이트 데이터셋
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]]) # 입력 데이터
y = np.array([0, 0, 0, 1]) # 출력 데이터
# 퍼셉트론 모델 학습
perceptron = Perceptron(input_size=2)
perceptron.fit(X, y)
# 학습된 가중치 확인
print("학습된 가중치:", perceptron.weights)
# 예측 결과 확인
print("AND 게이트 예측 결과:")
for inputs in X:
print(f"입력: {inputs}, 출력: {perceptron.predict(inputs)}")

이진분류가 안되잖아
그래서 그런게 아닌가 싶어
더 정확하게 알게되면
다시 얘기해줄게
뭐 일단은 어째든
다층 퍼셉트론에서는 활성화함수로 계단함수를 쓰지 않아
왜 그럴까?
우선 다층퍼셉트론에서는 역전파라는 과정으로
가중치를 업데이트 해
뭐라고 할까 시리즈 1탄에서 자세하게 다룬 내용이라
확인해보면 좋을 것 같아
그런데 역전파를 진행하려면
미분값이 필요한데,
계단함수는 미분을 할 수가 없어
미분 가능 조건을 한 번 찾아봐
자, 그래서
다층퍼셉트론에서는
활성화함수로 선형함수인
시그모이드 함수를 쓰게 돼
시그모이드 함수는
이렇게 생겼어

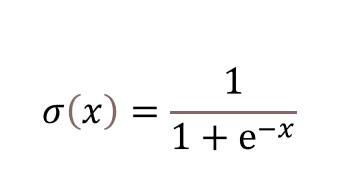
시그모이드 함수는
계단함수와 다르게 미분이 가능해
그리고 출력값이 0과 1 둘 뿐이 아니라
0에서 부터 1 사이의 연속적인 실수야
또한 출력이 항상 양수이고
출력의 평균값은 0.5야
하지만 시그모이드 함수에도 한계점이 있어
우선은 시그모이드 함수를 미분 해볼게


그러면 s' = s * (1-s) 라는 결과를 얻게 돼
이 그래프를 그려보면
이렇게 돼
파란색이 시그모이드 함수이고
주황색이 시그모이드 함수의 1차 미분값이야

시그모이드 함수의 한계점에는
기울기 소실 문제라는 것이 있어
영어로하면 gradient vanishing problem이지
역전파를 사용해서 가중치를 업데이트할 때,
각 계층에서 기울기(즉, 미분값)을 계산해서 전달해

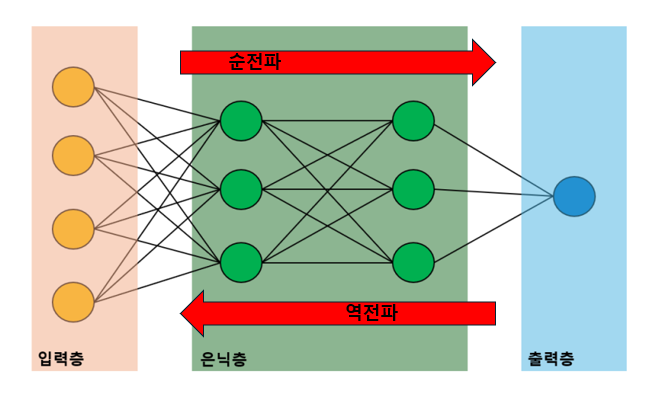

그런데 이렇게 전달이 되면서
기울기가 점점 작아져서
최종적으로 초기 계층의 가중치가
거의 업데이트가 되지 않는 문제가 발생해

시그모이드 그래프를 봐바
x가 매우 크면 y는 1에 무한히 가까워지게 돼
만약에 출력값이 1, 즉 s=1이면
시그모이드 함수의 미분값은
s'=s(1-s) 잖아,
그러면 s'=0이 되버려
또한,
x가 매우 작으면 y는 0에 무한히 가까워지게 되는데
이때도 시그모이드 함수의 미분값이
0에 무한히 가까워지게 돼
그러니까 x가 무한대로 크거나 작으면
미분값이 0에 가까워지게 돼
기울기를 통해 가중치를 업데이트하는데
기울기가 0이면 업데이트가 되지 않아
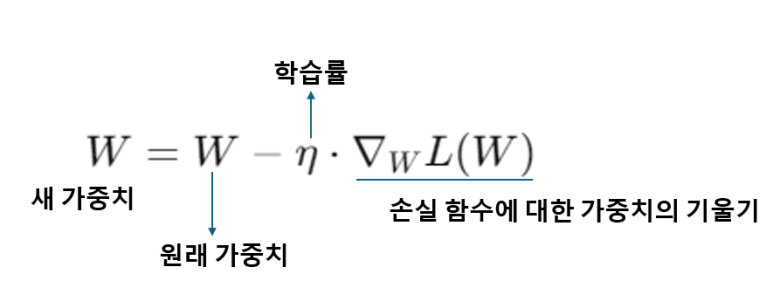
새 가중치=원래 가중치 - 0
이렇게 되겠지
또한 시그모이드 함수는

출력이 모두 양수여서
새 가중치=원래 가중치 - (양수)
이렇게 될 가능성이 높아
가중치를 업데이트할때
한쪽 방향으로만 편향된 결과를 가져올 수도 있어
이제는 하이퍼볼릭 탄젠트 함수에 대해 알려줄게


시그모이드 함수와 비슷하게 생겼지만
tanh 함수는 출력값이 -1에서 1까지야
출력값의 평균도 0이고,
입력값이 음수면 음수를,
입력값이 양수면 양수를 출력해
아까 시그모이드함수에서는
출력이 모두 양수여서
가중치를 업데이트 할때
한 방향으로 편향된 결과를
가져올 수 있다고 했는데
tanh함수는 그런 문제를 완화할거야
일단은
하이퍼볼릭 탄젠트함수를 미분해볼게

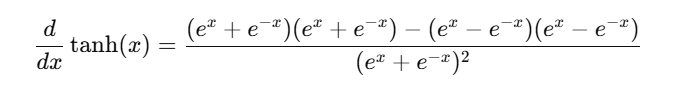

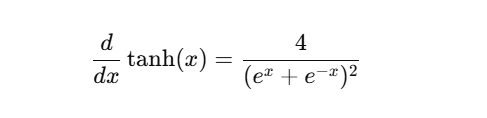
이것을 잘 정리하면
이렇게 돼


그래프를 그려보면
파란색이 tanh 함수이고
주황색이 1차 미분값이야

import matplotlib.pyplot as plt
import numpy as np
def tanh(x):
s=( np.exp(x) - np.exp(-x) )/ ( np.exp(x) + np.exp(-x) )
ds=1-s*s
return s, ds
X=np.linspace(-10,10,100)
Y1,Y2=tanh(X)
plt.plot(X,Y1,X,Y2)
plt.xlabel("x")
plt.ylabel("tanh(X)")
plt.show()하이퍼볼릭 탄젠트 함수도
시그모이드 함수보다는 조금 덜하지만
기울기 소실 문제가 발생해
x가 무한대로 클 때
y는 1에 가까워지고
t'=1-t*t 이므로
t가 1이라면
t'=1-1=0
그러니 x가 무한대로 클때
미분값이 0에 무한대로 가까워져
아까 시그모이드 함수에서 설명했던 것과 똑같아
자 이번에는 렐루 함수에 대해서 알아볼게
ReLU 함수는 Rectified Linear Unit의 약자야
수정된 선형 함수라는 뜻이지
렐루함수는 부분적으로 선형인 함수야
x>0 일때는 출력이 그대로 전달되고
x<=0 일때는 출력이 0이돼
입력이 0보다 크면 그대로 출력하고
0보다 적으면 그냥 0을 출력해


시그모이드 함수와 하이퍼볼릭 탄젠트 함수에서는
x가 무한대로 크거나 작을 때
미분값이 0에 무한히 가까워져서
기울기 소실 문제가 발생했잖아,
렐루함수가 x>0 일때의 미분값은 1이야
그래서 기울기 소실 문제를 완화할 수 있어
또한 렐루함수는 계산이 간단해
게다가 시그모이드랑 하이퍼볼릭 탄젠트함수와 비교했을 때
지수함수 계산도 없지
그래서 연산량이 적어서 계산을 빨리 할 수 있어
그런데 렐루함수는 음수일 때 출력값이 모두 0이라
입력값이 0 이하면 뉴런이 업데이트 되지 않아
그래서 Leaky ReLU 함수가 등장하게 돼
ReLU 함수에서 x<=0 일때 출력값이 0이 아니라
기울기가 살짝 있어

그리고 마지막으로
소프트맥스 함수를 소개할게
다중 클래스 분류 문제를 해결할때
출력층에서 주로 사용돼
회귀에는 항등함수 (입력을 그대로 출력),
분류에는 소프트맥스 함수를 사용한다고 해

def softmax(a):
exp_a = np.exp(a)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return ye^0 은 1이야
지수함수는 항상 양수의 값을 가져
그래서 x가 음수여도 소프트맥스 함수의 출력값은 양수야
입력값들을 0과 1사이의 값으로 변환하고
모든 출력의 합은 항상 1이 돼
큰 수는 더 커지고 작은 수는 더 작아지게 만들어
예를 들면 이런 식으로
[0.0, 0.0, 0.0, 0.0, 0.1, 0.0, 0.8, 0.0, 0.1, 0.0]
인덱스가 0부터 시작하니까
6 위치에 0.8이 있는 거잖아
그러니까 6일 확률이 80프로라는 거야
8일 확률은 10프로고
혹시 지금 뭔 소린지 잘 모르겠다면
저번 블로그 글에서 썼던 그림인데,

이런 식으로 출력층에 확률이 나오잖아

소프트맥스 함수는 출력을 확률로 나타내주면서
합이 1이라고 했잖아,
그러니까
입력층에 6 글씨 데이터를 넣었다면
여러 은닉층을 거치고
마지막에 출력층에 적혀있는 숫자들 있지?
각 숫자 (0~9)일 확률을 나타내는 거야
저 데이터의 글씨가 0일 확률,
저 데이터의 글씨가 1일 확률,
...
이렇게
6일 확률이 제일 높으면
저 글씨를 6이라고 예측하는 게 되는 것지
소프트맥스 함수는 softmax 함수잖아
부드러운 max 함수라는 거야
큰 값을 더 크게 만들지만은
다른 값들도 확률 분포에 포함시켜서
상대적인 중요도를 반영해
그래서
소프트맥스 함수를 적용한다고 해도
가장 큰 출력값의 위치가 변하는 건 아니야야
그냥 전체 합이 1이 되게 확률로 표현하게 되는 거지
그래서 모델이 실제 데이터에서 결과를 예측할 때는
소프트맥스를 생략하는 경우가 많다고 하더라
학습 단계에서는 사용하는 데
추론 단계에서 결과를 예측할 때는
정답 하나만 말하면 되잖아,
2 사진 보여주고 뭐냐고 그러면 '2' 라고 하던지
'3'이라고 오답을 말하던지.
소프트맥스 함수의 출력값이
y=np.array([0.0, 0.0, 0.0, 0.0, 0.1, 0.0, 0.8, 0.0, 0.1, 0.0])
이렇다고 하면,
제일 큰 출력값을 가진 위치인 6이 답이 되잖아
(0,1,2,3,4,5,6,7,8,9)
방금 말했듯이
소프트맥스 함수를 적용한다고 해도
가장 큰 출력값의 위치가 변하는 건 아니니까
굳이 소프트맥스 함수를 적용하지 않아도
제일 큰 출력값만 찾으면 되니까
결과 예측하는 단계에서는 생략해도 되는 것 같아
또한 소프트맥스 함수에는 지수함수가 있어서
연산량이 많아지니까 생략하면 좋은거고
활성화 함수에 대한 내용은
이정도로 마무리해야겠어
나는 사실 처음에 활성화함수면
다 통일되게 써야되는 줄 알았어
왜 그런 생각을 했지.. 몰라
근데 은닉층 활성화 함수랑
출력층 함수를
다르게 해도 되더라고^^
자 이제는 손실함수에 대해서 얘기해볼게

모델의 출력값이 예측값이잖아
예측을 했으면 정답이랑 맞춰봐야지
손실함수로 예측값과 정답을 비교해
오차를 알아내는 거야
이 오차가 손실함수의 값이 돼
그래서 예측값이 정답과 많이 다르다면
손실함수의 값은 커지는 거야
근데 우리는 오차가 적은 모델을 만드는 게 목표니까
손실함수의 값이 작은 게 좋겠지
손실함수에는 여러 종류가 있어
오늘은 평균제곱오차 (MSE)와
교차 엔트로피 함수에 대해서 소개할게
평균제곱오차는 주로 회귀 문제에,
교차 엔트로피는 주로 분류 문제에 사용을 한다고 해
일단은 평균제곱오차는 영어로
Mean Squared Error (MSE)라고 해
Mean은 평균이고 Squared는 제곱된 Error는 오차
라는 뜻을 가지고 있어

예를 들어서,

이 경우에서는 정답은
target=np.array([0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0])이렇게 되는 거고
(이렇게 하나만 1이고 나머지는 0인 걸 원-핫 인코딩이라고 그래)
y=np.array([0.0, 0.0, 0.0, 0.0, 0.1, 0.0, 0.8, 0.0, 0.1, 0.0])예측값은 이렇다고 가정하자
(소프트맥스 함수를 적용한거야)
def MSE(target, y):
return 0.5 * np.sum((y-target)**2)
첫번째는 예측값이 정답과 비슷하잖아
이때는 손실함수의 값이 작아
그런데 두번째처럼 차이가 많이 나게 되면
손실함수가 커지는 걸 볼 수 있어

식에 제곱이 있는 이유는 뭘까
예측값 - 정답을 하게 될 때
예측값이 정답보다 클 수도 있고
정답보다 작을 수도 있어
예측값이 정답에 얼마만큼 가까운 지를 구해야하는 데
그 차이를 다 합해줘야 되잖아,
조금 과정해서 설명하면
i =1 때 y-target = -7
i=2 y-target= 8 이라고 한다면
-7 이랑 8 을 더하면 1이 돼
사실은 둘 다 정답과 차이가 많이 나는 데
합한 결과는 1이 되버리는 거야
그래서 양수 오차와 음수 오차가 서로 상쇄되어
총 오차가 작게 나타나지 않도록
제곱을 해주면
음수도 양수로 변환이되어
오차가 상쇄되지 않아
그 다음은 교차 엔트로피 함수
Cross Entropy Error (CEE) 라고 해

def CEE(target, y):
delta=1e-7
return -np.sum(target * np.log(y+delta))

y는 예측값
예측값이라는 게 신경망의 출력이잖아
즉, 소프트맥스 함수의 출력이야
(마지막에 소프트맥스 함수를 사용하니까)
그래서 모든 출력의 합은 1이야
target은 정답값.
원-핫 인코딩을 사용하기 때문에
정답 하나 빼고는 다 0이 돼
그래서 식을 계산할 때
정답이 아니면
0 * log(x) 형태가 돼
0 곱하기 (무언가)는 0이기 때문에 0이 되잖아
그래서 정답일때의 출력이 전체 값을 정하게 되는 거야
정답일 때는 1.0 * log (0.8) 이 되니까
그래서 전체 값이 - (1.0 * log(0.8)) 이야
교차 엔트로피는
정답 레이블에 해당하는 예측값이
얼마나 정답에 가까운 지에 관심이 있어
보통 정답값 대신 목표값이라고 하고
예측값 대신 실제 출력이라고 하더라
코드에서 np.log(y+ delta)를 사용하는 이유는
log 0 이 정의되지 않기 때문이야

log x 그래프를 보면
x가 0에 가까워 질 수록 y는 무한히 작아지잖아
x가 0일때는 -∞ 로 발산한다는 것을 할 수 있어
그래서 np.log(y+ delta)를 해준거야
log 0 이 되는 걸 막기 위해서 아주 작은 값인 delta를 넣어준거야
자 이 정도로 마무리 해야겠어
다음에 누가 활성화 함수와 손실 함수가 뭐냐고 물어보면
이렇게 대답하면 좋겠어
그렇지만 시간이 조금 지나면 다 까먹겠지?
뭐 어째든,,
모든 그림, PPT로 제작
오타, 오류 제보
jyaenugu@naver.com
'딥러닝 > 뭐라고 해야될까 시리즈' 카테고리의 다른 글
| chapter 06 오토인코더가 뭐냐고 물어보면 뭐라고 해야될까 (0) | 2025.02.18 |
|---|---|
| chapter 05 RNN이 뭐냐고 물어보면 뭐라고 해야될까 (0) | 2025.01.30 |
| chapter 4 CNN이 뭐냐고 물어보면 뭐라고 해야될까 (0) | 2025.01.28 |
| chapter 3 경사 하강법이 뭐냐고 물어보면 뭐라고 해야될까 (0) | 2025.01.24 |
| chapter 1 딥러닝이 뭐냐고 물어보면 뭐라고 해야될까 (0) | 2025.01.22 |



