RNN이 뭐냐고 물어보면
뭐라고 해야될까
역시 chapter 01은 꼭 읽고 와야돼
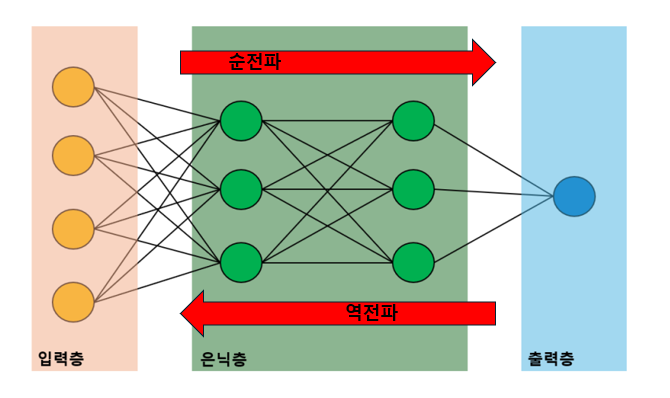
일단은 그때 보여줬던 그림을 다시 보여줄게

MLP (다층 퍼셉트론)은 피드-포워드 신경망이야
(feed-forward neural network)
CNN 또한 피드-포워드 신경망이야
그게 뭐냐면 순방향이라는 거야
데이터가 한 방향으로만 흐르는 거야
입력에서 출력으로
여기서 좀 헷갈렸던 게
역전파는 뒤로 가잖아? 였어

근데 역전파는 신경망이 아니라 학습을 시키는 알고리즘이야
순전파만 있으면 예측만 가능한거고
역전파를 이용해서 모델을 학습시키는 거야
그치만 이 모델 자체는 입력-> 은닉층 -> 출력
이렇게 한 방향으로 흘러가는 거야
chapter 01에서는 얘기를 안하고 있다가
갑자기 이 얘기를 하는 이유는 뭐냐면
RNN은 이것과 다르기 때문이야

RNN은 이렇게 순환해
RNN이 (Recurrent Neural Network)거든
여기서 recurrent는 순환이라는 뜻이야
순환이라는 게 뭔지 이해가 어렵지?

h1 h2 h3 h4 h5
이렇게 있으면
h1 + x2 => h2
h2 + x3 => h3
h3 + x4 => h4
과거의 출력(h t-1)이
현재의 출력에 영향을 주게 되는 거야
조금 더 자세히 볼게

RNN 구조 그림을 이렇게 바꿔서 표현해볼게
그러면 이렇게 순환구조를 펼쳐볼 수 있어


x는 입력 데이터고 t는 시간을 뜻해
입력 데이터인 x1과 그 전 계층의 출력인 h0 을 받아서
h1 을 계산해
RNN의 특징은
x1 뿐 만이 아니라
그 전의 출력인 h0까지 전달 받아서
h1을 계산해준 다는 거야
이전의 데이터를 기억하면서 가는 거지
이렇게 나타낼 수도 있어

더 복잡해졌지만
t=1 일때를 보면
x1 + h0 => h1 이 되는데
h0은 t=0일때의 출력이야
그게 h1에 영향을 주게 되는 거를 볼 수 있어



다시 말하지만
RNN은
이전의 데이터를 기억하면서 가는 거야
순서가 중요한 데이터들이 있어
이걸 순차 데이터(sequence data)라고 해
그리고 특히 시간 순서가 중요한 데이터를
시계열 데이터라고 해
예를 들면 "music"이라는 단어는
알파벳의 순서가 중요해
순서가 중요하면
이전의 데이터가 뭐였는 지 기억하고 있어야 돼
그런데 피드 포워드 신경망으로는
멀리 떨어진 과거의 데이터를 잘 기억하지 못해
그래서 RNN이 필요해
RNN은 이전의 데이터를 기억하면서 가잖아
음 feed-forward 신경망이 이런 느낌이였다면
(입력으로 cat 입력층을 잘 봐 글자를 적어놨어)

RNN은 이렇게 되는 거지

자 이번에는 RNN의 역전파에 대해서 알아볼게
우선 가중치를 어떻게 공유하는 지 잘 봐


시점이 있어서 조금 더 복잡할 뿐
chapter01에서 설명한 MLP의 역전파랑 비슷해
chapter01에서 했던 거를 다시 보여줄게

RNN도 똑같이 하는 거야
다만, 밑에 있는 그림은 t=1 시점일 때인데
t=0 시점까지 포함하고 있기 때문에
업데이트를 하면 t=0 시점에도 영향을 주게 돼

t=2 일때는 이렇게 돼

이건 t=0과 t=1에도 영향을 주게 되는 거지
그리고
이거는 그냥 내가 이해한 거로
직접 써본건데
제대로 이해한지를 모르겠어서
틀릴 가능성이 굉장히 많아...
그래도 대충 느낌을 봤으면 좋겠어서 넣어봤어

시점별 기울기를 다 더해서 업데이트를 한다고 하더라고
RNN의 역전파를 BPTT라고 불러
(Backpropagation Through Time)
음 뭔가 만족할 수준으로는 이해를 못한 것 같아서 아쉽네
나중에 더 공부를 하다가 추가할 내용이 있으면 추가할게
자 RNN에는 문제가 있어
기울기 소실 문제야

아까 여기서 tanh는 활성화 함수라고 했잖아
chapter 02에서 다뤘던 하이퍼볼릭 탄젠트 함수야
그때 기울기 소실 문제에 대한 내용을 말한 적이 있어
시그모이드 함수에서 자세하게 설명했지만
하이퍼볼릭 탄젠트 함수도 기울기 소실 문제가 있어
다시 읽어보면 좋을 것 같아
""""
시그모이드 함수의 한계점에는
기울기 소실 문제라는 것이 있어
영어로하면 gradient vanishing problem이지
역전파를 사용해서 가중치를 업데이트할 때,
각 계층에서 기울기(즉, 미분값)을 계산해서 전달해

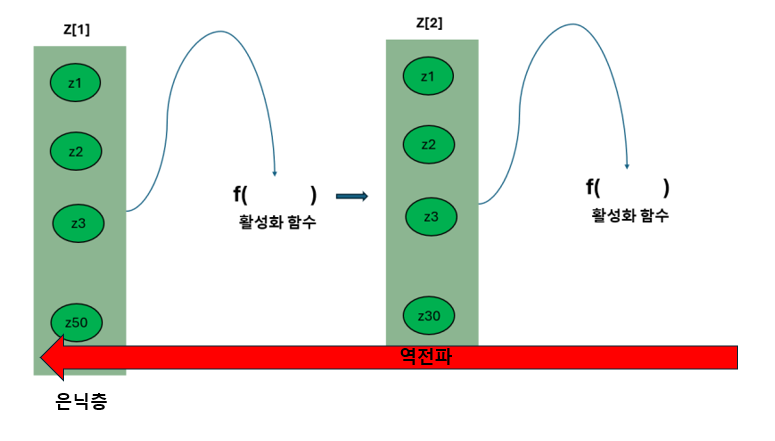
그런데 이렇게 전달이 되면서
기울기가 점점 작아져서
최종적으로 초기 계층의 가중치가
거의 업데이트가 되지 않는 문제가 발생해

시그모이드 그래프를 봐바
x가 매우 크면 y는 1에 무한히 가까워지게 돼
만약에 출력값이 1, 즉 s=1이면,
시그모이드 함수의 미분값은
s'=s(1-s) 잖아,
그러면 s'=0이 되버려
또한,
x가 매우 작으면 y는 0에 무한히 가까워지게 되는데
이때도 시그모이드 함수의 미분값이
0에 무한히 가까워지게 돼
그러니까 x가 무한대로 크거나 작으면
미분값이 0에 가까워지게 돼
기울기를 통해 가중치를 업데이트하는데
기울기가 0이면 업데이트가 되지 않아
""""
그리고 이어서
"""

하이퍼볼릭 탄젠트 함수도
시그모이드 함수보다는 조금 덜하지만
기울기 소실 문제가 발생해
x가 무한대로 클 때
y는 1에 가까워지고
t'=1-t*t 이므로
t가 1이라면
t'=1-1=0
그러니 x가 무한대로 클때
미분값이 0에 무한대로 가까워져
아까 시그모이드 함수에서 설명했던 것과 똑같아
"""
특히 RNN에서는 mlp 보다 계산을 해야될 게 많잖아
게다가 일단 이 그림을 이렇게 돌려보면

가중치를 어떻게 공유하는 지 다시 잘 봐바


이거잖아
근데 가중치를 이렇게 공유하기 때문에
역전파를 할때 Wh가 계속 곱해져
이게 쌓이고 쌓여서
역전파를 할 때 하이퍼볼릭 탄젠트 함수의 미분값이
여러 번 곱해지면서 문제가 발생돼
만약에 Wh가 1보다 크면
기울기가 엄청 커지겠지
그럼 기울기가 폭발하고
Wh가 1보다 작으면
곱해지면서 값이 점점 작아지면서
기울기 소실 문제가 발생돼
그렇게 되면
먼 거리에 있는 입력을 기억하지 못하게 되는 거야
이런 문제를 장기 의존성 문제라고 해
이 문제를 LSTM이 해결해
LSTM은 Long short-term memory야
이것도 순환 신경망이지
어떤 차이점이 있는 지 부터 알아야겠지?
우선 이건 아까 계속 설명하고 있었던
RNN이야


이제 LSTM을 보여줄게


LSTM는 게이트가 추가된 RNN이야
3개의 게이트가 있지
output gate
forget gate
input gate
하나씩 설명해줄게
우선 forget gate야
얼마만큼 기억을 삭제할지 결정하는 거야
시그모이드 함수가 게이트라고 했잖아
아까 그림에 적어놓은 거 안읽고
그냥 지나쳤다면 다시 꼭 읽어봐
중요한 정보가 아니라면
모두 기억하고 있을 필요가 없잖아
forget gate는 기억을 삭제해

그리고 기억 셀을 업데이트를 해줄 게
forget gate를 통해 나온 값을
곱해서 일부 기억을 삭제해

기억 셀이 뭔 지 말을 안해주고 넘어갔지?
LSTM의 또 다른 특징은
ct라는 거야
ct는 기억 셀이야
셀의 상태를 나타내
셀 이라는 게
각 시점에서 정보를 저장하고 업데이트를 하는
단위라고 생각하면 될 것 같아
과거부터 t 시점까지 필요한 모든 정보를
기억하고 있어
그 다음은 input gate야
새로운 정보를 저장하기도 해야되잖아
그때 이 정보가
얼마만큼의 기억할만한 가치가 있는 지
결정을 하는 거야

그리고 업데이트 과정
input gate의 출력인 i와
활성화 함수를 거친 g의 원소별 곱 결과를
기억 셀 ct에 업데이트 시켜줘

마지막으로 output 게이트야
어떤 정보를 다음 시점의 셀로 출력을 할 지를 결정해

ht는 출력이야
ct는 LSTM 안에서만 쓰고
다른 계층으로는 출력되지 않아
자 LSTM이 RNN의 문제를 해결하기 위해서
만들었다고 했잖아
RNN에서는

역전파를 할 때
이렇게 같은 가중치가 계속 곱해지면서 문제가 생겼지
LSTM에서는 RNN에
게이트와 기억 셀 c를 추가했잖아
이게 이런 느낌으로 추가되는 거야

LSTM은 구조가 좀 복잡해지잖아
RNN에 비해서.

게이트가 얼마만큼 정보를 기억할 지 결정을 하기 때문에
매번 값이 달라져
forget 게이트에서는
기억하지 않아도 될 기억 셀의 원소의
기울기를 작게 만들고
그리고 기억해야 될 기억 셀의 원소의
기울기는 약화되지 않은 채로 다음으로 전달했잖아
이렇게 매 시점마다 다른 값이 만들어지고
이 값을 이용해서 원소별 곱을 계산하기 때문에
곱셈이 누적되지 않아
자 이제 LSTM까지 알아봤으니
마무리해야될 시간이 온 것 같아
누가 RNN이 뭐냐고 물어보면
이렇게 대답을 해야겠어.!
그런 날이 올 때는
지금보다 공부를 더 한 상태여서
이것보다 더 잘 설명할 수 있으면 좋겠다
음 현실은 이거를 다시 참고하지 않으면
아무 말도 못할 것 같지만
어째든,,
모든 그림, PPT로 제작
오타, 오류 제보
jyaenugu@naver.com
https://github.com/hanseohee031
hanseohee031 - Overview
hanseohee031 has 7 repositories available. Follow their code on GitHub.
github.com
'딥러닝 > 뭐라고 해야될까 시리즈' 카테고리의 다른 글
| chapter 04 CNN이 뭐냐고 물어보면 뭐라고 해야될까 (0) | 2025.01.28 |
|---|---|
| chapter 03 경사 하강법이 뭐냐고 물어보면 뭐라고 해야될까 (0) | 2025.01.24 |
| chapter 02 활성화함수와 손실함수가 뭐냐고 물어보면 뭐라고 해야될까 (0) | 2025.01.23 |
| chapter 01 딥러닝이 뭐냐고 물어보면 뭐라고 해야될까 (0) | 2025.01.22 |



